| |
 |
|
|
|
| |
| Fourier series |
| |

The method of Fourier series is a general method to express any repeating wave form in terms of a linear combination of sine and cosine functions. Square waves, sawtooth, and other standard forms are shown as examples. But, the method is completely general and can be used to represent any repeating wave form. One can view the Fourier series of a wave that has changing amplitude in time as a collection of components with a given frequency (from the sine and cosine functions required to represent it). In this sense, one can see a Fourier series as a kind of "transform" from time to frequency space. A similar relationship exists in the transform from distance to wave number space.
Fourier transform
The Fourier series is a mathematical representation, which forms the foundation for the Fourier transform. In a Fourier transform the wave form does not need to be repeating function. The procedure for finding sine and cosine terms, also known as the Fourier components, of a wave is generalized as an integral. The components are combined into a single transform function,
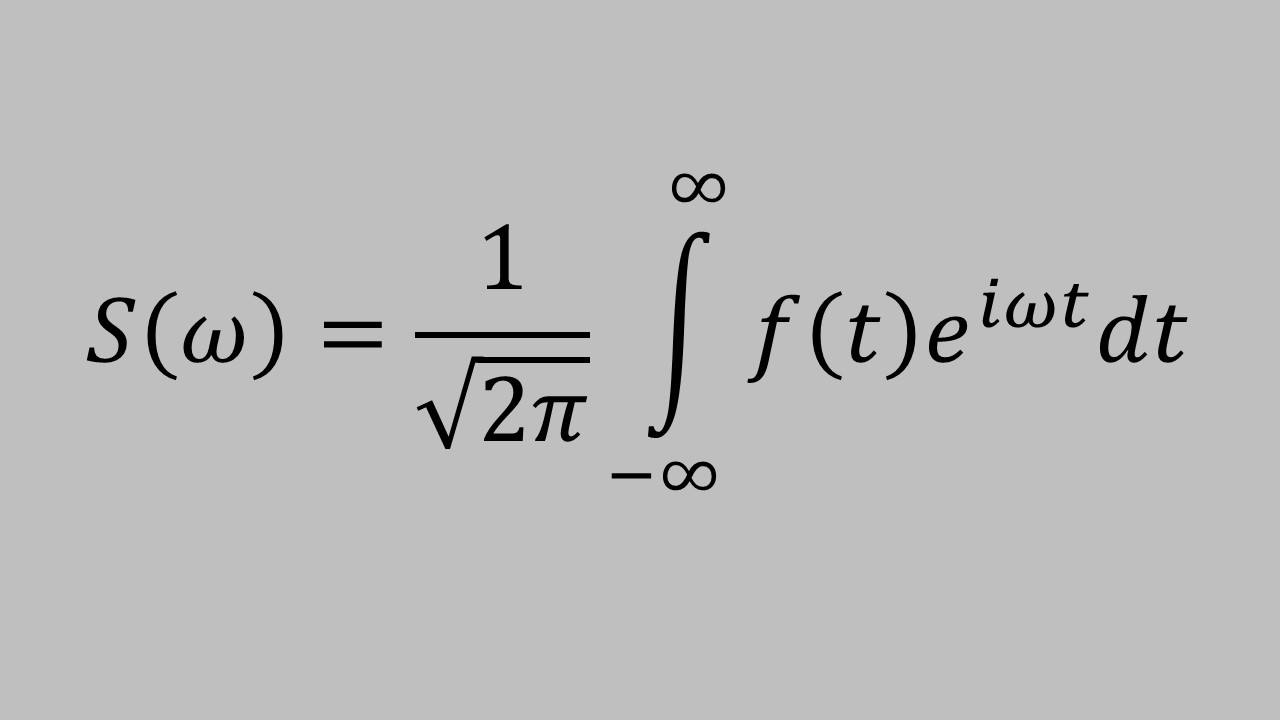
Fast Fourier transform
Nyquist frequency and aliasing
According to Fourier analysis the information content of a wave form can be represented in terms of the frequency components. In practical applications we will digitize the signal at some digitization rate. We can ask how many data points we need in order to accurately represent the signal. Or put another way, what is the minimum number of points needed to represent a the Fourier component of highest frequency? The answer is surprising. We can repesent that wave using two points per wavelength. Those points need to be the peak and trough of the wave.
Analytical Expressions: Gaussian and Lorentzian Fourier transforms
The Lorentzian and Gaussian are the two wave forms that have the most wide spread application in spectroscopy. A Lorentzian is obtained byt he Fourier transform of an exponential.
Fourier transform applications
Fourier transform application in crystallography
Fourier transform application in Nuclear Magnetic Resonance (NMR)
Fourier transform application in Fourier Transform Infrared spectroscopy (FTIR)
| |
| |
|