The quantum theory clearly had to apply to the hydrogen atom. The Rydberg model showed that there were quantized transitions. However, this problem was not immediately solved using a wave equation. The mathematical solution was quite involved. First, a different approach was used that is known as the semi-classical method. In 1913 Niels Bohr proposed a planetary model, in which the electron moved in orbits about the proton (nucleus). He used quantization of angular momentum to introduce Planck's constant into the problem. His solution accurately predicted the Rydberg constant. This was a great triumph. However, his method could only be applied to hydrogen. All other atoms were intractable.
The Schrodinger equation for hydrogen
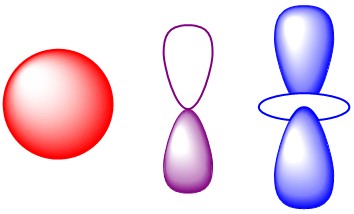
The wave equations can be applied to the hydrogen atom. Using spherical polar coordinates there is an exact solution. The wave functions for the hydrogen atom are the most important solutions in all of quantum chemistry. The shapes of the angular part, which arethe familiar s, p, d and f orbitals form the basis for approximate methods that permit calculation of the energy and other properties of atoms and molecules. THe hydrogen atom is the only atom, for which there is an exact solution, but that solution is the starting point for all approximate solutions. The energies of the hydrogen atom agree with experiment and are equal to he result obtained by Bohr using semi-classical methods.
Atomic absorption and emission as a quantum effect
There were other unexplained phenomena around the year 1900 that also began to make sense if one accepted the idea that light could be absorbed as a particle. There were well-defined emission lines of hydrogen that had been studied by a number of scientists. Rydberg combined these observations and noticed a pattern that suggested that the energy levels must depend on an integer value. The individual energy levels of hydrogen appear to follow the pattern E = -R/n2, where R is a constant known as the Rydberg constant. For hydrogen R is equal to 13.6 electron volts (eV) and n is an integer greater than zero. For other nuclei we can write E = -ZR/n2 where Z is the nuclear charge. The lines the emission spectra fit a pattern of emission between different states with two different quantum numbers (see Quantum transitions)
The wave equation in quantum mechanics
- There is no ballistic motion in quantum mechanics since particles behave like waves and therefore the equation of motion is a wave equation.
- Instead of defining precisely where particles are located in space (i.e. using coordinates x, y and z), the solution of the wave equation is a wave function that can be used to calculate the probability for the particle to be in a given region of space.
- The probability can be calculated from the square of the wave function. The square will involve a product of the complex conjugate if the wave function is complex. The wave function must be normalized in order for the probability to be meaningful.
- The wave function can also give properties of the wave function solution in the form of operator equations. For example, the energy can be calculated using an energy operator, known as the hamiltonian. The momentum can be calculated using a momentum operator, and so on.
|