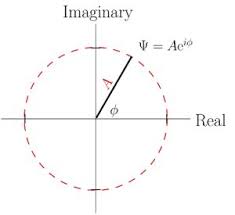
The use of the complex plane provides a mathematical method to discussion of rotations. There are two related ways to designate any point on the plane 1.) using Cartesian coordinates (x = real and y = imaginary) and 2.) using polar coordinates where the location is given by Ae^{i phi}. We can see that this representation of the location of the number provides a rotation angle phi. The rotation angle is relative to the x-axis in this case. However, if we were to change the rotation angle we would define a different point at the same distance from the origin. In other words the designation A e^{i phi} is a representation of the rotation of a point about the origin around a circle of radius A. This realization gives us the tools we need to define rotations in the manner used in NMR and optical spectroscopy as well as quantum mechanical operators.

Applications of complex numbers

Significance of phase

We can also give a physical interpretation to complex numbers. From the definition of a complex plane we see that the real and imaginary axis are orthogonal to each other. Thus, they are 90^o out of phase with respect to one another. As a general rule we can view the real and imaginary parts of a complex response function as giving the complete response in terms of in-phase and out-of-phase interactions. An example is given by the interaction of light and matter. If light polarizes matter, changes its direction and passes through matter we call this dispersion. Dispersion is wavelength dependent, but it is in-phase in the sense that the motions of the electrons follow the radiation and the radiation moves through matter without being absorbed (or incurring any losses). One the other hand absorption of radiation during interaction with matter can be viewed as an out-of-phase interaction.

Matrix Applications

Savitzky-Golay Analysis

Singular Value Decomposition

read more…