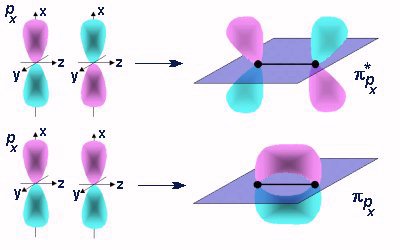
Molecular orbitals can only be obtained using approximate methods. There is no exact solution. A key breakthrough was achieved using the Hartree approximation, which permitted the N-body problem to be reduced to a collection of single electron interactions. In essence, the idea is that we wil solve for the motion of each electron in the field of all of the other electrons. This permits the N-body problem to be wrtitten as a set of linear equations in each electron. The exact solution of the hydrogen atom provides an important starting point as well since it provides a functional form for the wave functions on all atoms. Imagine placing a set of hydrogen-like orbitals on each nucleus of a molecule. Then the problem of forming molecular orbitals is to determine the coefficient of each of these basis orbitals. This is the essence of the LCAO-MO approach. Here we will instroduce the approach using a generalized variational principle for any number of electrons. Then we will consider applications of group theory that help simplify the problem. These are useful for understanding the structure and applications of molecular orbitals as well.
Huckel theory
Huckel theory uses the LCAO-MO result to calculate the energy of the pi-system of linear and aromatic molecules. That result is known as the secular determinant, det|H - ES| = 0. Huckel theory is a semi-empirical theory, which means that we use parameters to estimate the energies and resonance integrals. The matrix elements Hij are obtained from these parameters. Even with this approximate method there is a roadblock for analytical solution. The dimension of the Huckel matrix is equal to the number of atoms in the pi-system. Often this means that it is not possible to diagonlize the matrix (which is required to solve the equation for the determinant. Expanding a 6x6 matrix for benzene is simply too time consuming. These methods were developed prior to the advent of the computer. Today we still use these methods for their intuitive simplicity. We can overcome of the problem of dimensionality by use of symmetry. In the case of benzene the 6x6 matrix is converted into two 2x2 and two 1x1 matrices, known as symmetry blocks. Only the linear combinations of symmmetry adapted orbitals contribute to a particular block. Thus, relatively large molecules can be solved by hand. This helps us to obtain insight into the much larger problems that are solved by computer today.
Limitations of the Huckel approach
Clearly the Huckel method is simplification. If one wants to calculate realistic energies it is necessary to develop ab initio methods that are based on calculation of resonance integrals using the electrostatic potential For example, geometry optimization and frequency calculation require a more realistic estimate of bonding than is possible using semi-empirical methods. The goal of Huckel theory in today's applications is to give a qualitative picture and an understanding of the methods. Once a student can picture the steps needed to calculate the energies and the eigenvectors (i.e. coefficient of the MOs), those same processes can be understood in computer outputs from Hartree-Fock or Density Functional Theory methods.
|