General example of a derivation of the free energy of reaction from the chemical potential

This example can be extended to a general case, using an idealized reaction:

aA + bB ßà yY + zZ

(1)

The equilibrium constant for this gas phase reaction is,

(2)

We will derive this form of the equilibrium constant in the following. At constant T and P we will write the total Gibbs energy as

(3)

In the general case we can write

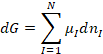
(4)

where we have used capital I to mean component I. In order to consolidate the changes in moles we note that we can write all of the molar changes dn_i in terms of an overall reaction coordinate dn,

for products, and

for reactants. The products have a positive sign since they are typically being formed and the reactants have a minus sign since they are being consumed. Thus, for the hypothetical reaction above we have

(6)

In Eqn. 8.6.21 the dn represents an overall reaction progress variable. It is multiplied by the stoichiometric coefficient of each reactant and the sign is positive for products and negative for reactants. We have converted the change in each individual reactant or product into a global variable that measures how far the reaction has progressed. We do not yet know how far the reaction will progress. Equilibrium may mean that there is a balance of reactants and products and dn may be either close to zero (mostly reactants) or close to 1 (mostly products), by the time the reaction is complete. We now define D_rxnG:

(7)

This definition is unique to chemistry and lacks a formal justification in the field of mathematics. To equate a partial derivative quantity with a macroscopic change is not formally defined. Yet, this step has been used to define the free energy change for more than 100 years. The importance of Eqn. 8.6.22 is when we realize that it permits us to use the chemical potentials of individual components to define the collective free energy of a chemical process. We apply the chemical potential for component I:

(8)

We can write the Gibbs energy as:

(9)

and use the chemical potentials for reactants:

and products:

(10)

which can be substituted into Eqn. 9,

(11)

to obtain

(12)

where

(13)

and

(14)

We note that this gives use the formal definition of the standard free energy of reaction, , in terms of the chemical potential of the reactants and product. The reaction quotient, , follows directly from the fact that the reaction stoichiometry becomes raised to the power of the coefficient inside the logarithm.