Derivation of free energy of reaction from the chemical potential

The most general expression for the dependence of the free energy on temperature, pressure and composition is

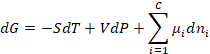
(1)

Note that we can see that the number of degrees of freedom in the system is F = C + 2, where C is the number of components and the 2 additional degrees of freedom are temperature and pressure. At constant temperature and pressure this becomes

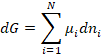
(2)

To see how this equation can be implemented let’s consider a gas phase reaction as an example. We will use a textbook example:

N₂O₄ (g) = 2 NO₂ (g)

(3)

The equilibrium constant for this gas phase reaction is,

(4)

At constant T and P we will write the total Gibbs energy as

(5)

In Eqn. 5 the dn represents an overall reaction progress variable. It is multiplied by the stoichiometric coefficient of each reactant and the sign is positive for products and negative for reactants. Specifically, we use the reaction stoichiometry in 8.6.2 to obtain the factor 2 for NO₂.

We have simply converted the change in each individual reactant or product into a global variable that measures how far the reaction has progressed. We do not yet know how far the reaction will progress. Equilibrium may means that there is a balance of reactants and products and dn may be either close to zero (mostly reactants) or close to 1 (mostly products), by the time the reaction is complete.

We now define D_rxnG:

(6)

Note that we will use D_rxnG and DG interchangeably. The mathematical justification for Eqn. 6 is flimsy at best. On the left hand side we have D_rxnG and on the right hand side we see a derivative. Nonetheless, this expression has been used for many years to justify the relationship that determines the direction of spontaneous change of chemical reactions.

The quantity in Eqn. 6 is D_rxnG but it is not D_rxnG^o! D_rxnG^o (which is most often written DG^o) is the standard free energy change, means that it is the free energy change under relative to the standard state, which is 1 atm of pressure or 1 M of concentration in solution. If we now apply the pressure dependence for one component,

(7)

to a multicomponent system:

(8)

These two expressions are essentially identical. The chemical potential, m_i, is nothing more than a molar free energy for a particular reactant or product in a reaction. See the example of NO₂ above. Using Eqn. 6 We can write the Gibbs free energy as:

(9)

and use the chemical potentials:

(10)

which can be substituted into Eqn.9,

(11)

to obtain

(12)

where

(13)

and

(14)

The quantity Q is called the reaction quotient. It looks like the equilibrium constant, but there is a subtle difference. Q is not required to be the equilibrium ratio of reactants and products. For example, if there is an excess of N₂O₄ initially, then may be large so that Q << K. In that case and the reaction will proceed to produce products. The value of Q will change until Q = K. At that point, and the reaction will have reached equilibrium. Thus, at equilibrium we write,

(15)

Thus,

(16)

which can also be written

(17)

The change DG is the change in the Gibbs energy function. It has three possible ranges of value:

DG < 0 (process is spontaneous)

DG = 0 (system is at equilibrium)

DG > 0 (reverse process is spontaneous)

On the other hand DG^o is the standard molar Gibbs energy change for the reaction. It is a constant for a given chemical reaction.