Protein folding

Protein folding is a relatively complex process because the linear peptide chain has order that leads to folding of specific amino acids on the interior and others on the exterior of the folded protein. We can examine the contribution to the free energy of the various amino acid side chains and secondary structure elements in order to help determine the rules for protein folding. While this is long from a solved problem, much progress has been made in the understanding of the energetic and kinetic contributions made by specific structures. First, we consider the globar problem of protein folding. Subsequently, we will decompose the problem into its component parts by considering, hydrogen bonding, electrostatic, and hydrophobic interactions.

The global consideration for protein folding starts with the consideration of a two-state protein folding model. While this is probably a simplification for most protein folding problems, the existing experimental data are consistent with a two-state model in the majority of cases. Therefore, we are justified in using it. It is certainly the most appropriate model to explain the issues in protein folding.

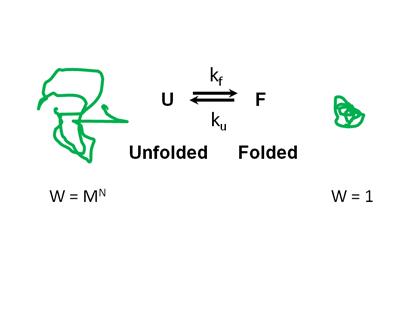
Figure 15.1. Depiction of the two-state model for protein folding.

The two-state model implies that an equilibrium exists between the folded and unfolded conformations. The equilibrium constant is:

(1)

However, we often measure the relative amount that is folded, i.e. the fraction of folded protein, ff. Of course, the fraction of unfolded protein fu is just 1 – ff. Therefore, we can also write the equilibrium constant as

(2)

Solving for ff we obtain

(3)

We can use our knowledge of the relationship of K and DG^o to write

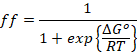
(4)

which can also be expressed as

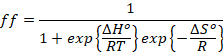
(5)

The temperature at which the protein is 50% folded can be defined as T_m the melt temperature.

At T_m , DG^o = 0 or T_m = DH^o/DS^o.

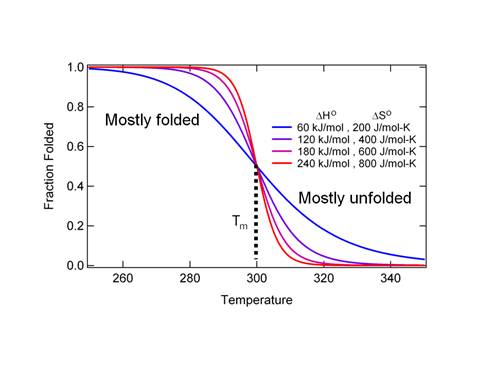
Figure 2. An equilibrium melt curve. T_m is called the melt temperature.

It is the temperature at which the protein begins to unfold.

Figure 2 shows a compensation of DH^o and DS^o such that the T_m is 300 K in all cases. The greater DH^o and DS^o the steeper the curve. Most realistic cases have relatively small values of

DH^o so that the curves are shallow (see the blue curve). A typical protein contains a few salt-bridges, several hundred hydrogen bonds and several thousand van der Waals interactions. In spite of all these interactions proteins are only marginally stable. Typical DG values for folding of proteins are in the range of -5 to -15 kcal/mol i.e. not much greater than the energy of 2 or 3 hydrogen bonds. This is because of several effects which cancel each other out. The enthalpy change of protein folding (DH) is dominated by hydrogen bonds. In the unfolded state the polar groups of the protein will H-bond to solvent molecules and in the folded state these polar groups will H-bond with each other. Hence the overall enthalpy change on folding is small. The hydrophobic effect is thought to make the largest contribution to DG that stabilizes the folded state. The hydrophobic effect attributes the poor solubility of non-polar groups in water to the ordering of the surrounding water molecules causing them to form an ice-like cluster. This is shown in Figure 3.

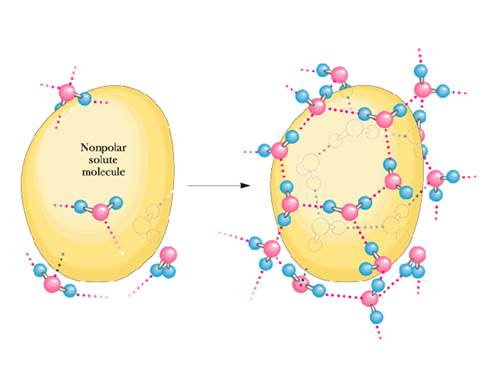
Figure 3. The hydrophobic effect. The left panel shows the unfavorable interactions of water with a hydrophobic object. O-H interacts strongly with oxygen lone pairs, but not C-H groups on hydrophobic molecules. The right panel shows water with an organized structure around a hydrophobic solute. The water molecules have rotated to avoid contact of O-H groups with the solute.

On the other hand, the conformational (or configurational) entropy is the largest destabilizing force. The number of possible conformations in the unfolded state is large. We have shown in a previous chapter that the number of accessible states (conformations) W = M^N where M is the number of conformers for each monomer and N is the number of monomers in the biopolymer. In the folded state there is a relatively small number of conformations. In an ideal folded protein W = 1, i.e. there is a unique conformation. In that case the conformational entropy can be estimated to be

(6)

Hence,

(7)

which is a significant contribution. In fact, the entropy issue is a major issue in protein folding. It was first raised in 1968 by Levinthal in a famous article that discussed the consequences of the statistical nature of protein conformations. Assuming that the protein searches randomly for the correct conformation, the number of states the must be sampled is enormous. For a protein like human myoglobin with 160 amino acids and an average of 6 conformations per side chain, the total number of conformations is W = 6¹⁶⁰ 5 x 10¹¹⁶! The kinetics of this entropic contribution presents a paradox, known as the Levinthal paradox. Even with a ultra-rapid random search it would take longer than the age of the universe to find the folded conformation. Is the large negative entropy overcome in a single step or is protein folding a more gradual and complex process. We will revisit this question when we talk about kinetics. However, at this point it is clear that conformational (statistical) entropy is the dominant force that leads to protein unfolding. Moreover, since it is an entropy, it is temperature dependent.

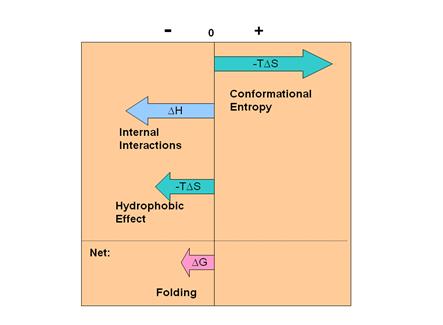
Figure 4. Summary of contributions to the free energy of protein folding.

Figure 4 shows that the balance of the various contributions to DG^o leads to a near cancellation such that DG^o is quite small. Under physiological conditions D_foldingG^o < 0 for proteins that fold in the cell. However, DG^o decreases in magnitude as the temperature increases. When DG^o = 0 the protein is in equilibrium with its unfolded state. We often call this the “melt” temperature, T_m, as shown in Figure 2. Above this temperature proteins unfold or denature. Protein unfolding is important in disease. For example, when you run a temperature, your elevated body temperature can cause viral or bacterial proteins to unfold. This compromises the ability of the invader to further infect the body. Protein folding can also be harmful as in the case of Alzheimer’s disease, which is caused by plaques that form with the Ab peptide aggregates in the vicinity of a nerve cell.