Derivation of the kinetic equation for CO recombination to deoxy Mb

One can assume that the photolyzed product Mb:CO is present initially as shown in the figure (His-FeP:CO or Mb:CO). There are two pathways shown with rate constants k_gem and k_esc. gives rise to the following rate scheme.

These equations cannot be solved exactly. However, we can solve the equation for the geminate state, Mb:CO, which is immediately produced by photolysis. The result is,

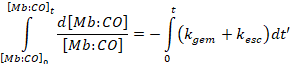
Since the rate constants k_gem and k_esc >> k_bi, we can approximately the rate of formation of MbCO and the deoxy Mb states as

Which leads to,

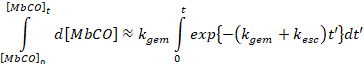
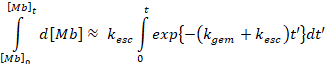
And

According to the myoglobin rate scheme there is a quantum yield for both geminate recombination and escape. These are,

Finally, we can determine the rate of depletion of the deoxy state (i.e. bimolecular recombination) from a separate equation,

Solution of the rate equations Combining these equations leads to the overall time course

where the prime indicates that this is a pseudo-first-order rate constant, . The pseudo-first order rate constant has the appearance of a first order process at a fixed concentration of CO. Figure 1 shows how the rate differs as the CO concentration is varied by a factor of 10.

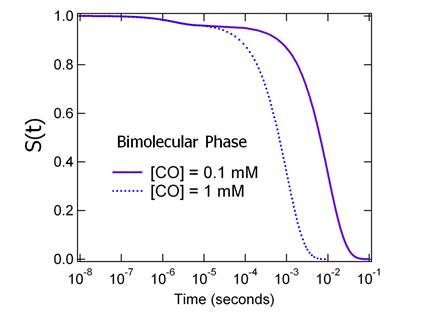
Figure 1 MbCO recombination kinetics showing the difference between the geminate and bimolecular phases. The bimolecular phase is pseudo-first order.