Spectroscopic studies of myoglobin thermodynamics and kinetics

Myoglobin has been dubbed the “hydrogen atom of biophysics”. It was the first protein crystallized and has been studied by every conceivable physical method. Myoglobin is the protein in muscle that is responsible for oxygen binding and storage. It is composed of 8 a-helices in the globular structure shown below. The red, purple or brown color of myoglobin arises from the heme group, which can exist in two oxidation state, ferrous (Fe²⁺) and ferric (Fe³⁺).

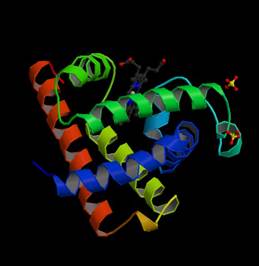
Figure 1. Structure of myoglobin from Sperm Whale.

Ferrous myoglobin can exist in a ligand bound state (e.g. Fe-O₂, Fe-CO, or Fe-NO), or in the deoxy state. Deoxy myoglobin is five-coordinate and the ligand-bound states are six-coordinate. We are often interested in measuring binding to myoglobin in the presence of a given partial pressure of a gas. To relate the concentration of the gas in solution to the pressure we use Henry’s law.

(1)

where K_H is the Henry’s law constant, which is also the equilibrium constant for gas solubility. The binding in solution is governed by the interaction of the ligand with iron. The dissolved CO gas can diffuse into the protein and bind to the iron as shown in the cryogenic X-ray crystal structures shown in Figure 1.

.1.1 Structural forms of carbonmonoxy myoglobin

Figure 2 was obtained at 20 K where the protein is sufficiently rigid that the CO cannot escape. However, the CO can be photolyzed, which means that the Fe-CO bond is broken by laser irradiation. Specifically, the heme group can be photoexcited in resonance with its p-p* transition, as shown in Figure 4 where the absorption spectra of two forms of the heme group are shown. The bound form of CO is called MbCO, shown in Figure 2 as the red form of the protein. The photolyzed form, Mb:CO, is shown as the purple form in Figure 2. The deoxy form is crystallized without any CO and is shown as the blue form.

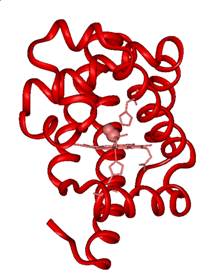
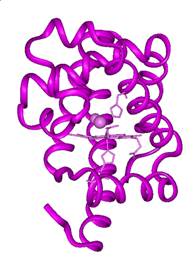
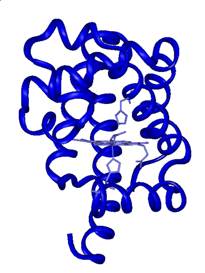
Figure 2. Cryogenic X-ray crystallographic structures of MbCO (red), Mb:CO (purple) and Mb + CO (blue).

The three forms are shown superimposed in Figure 3. Figure 3 also shows an expanded view of the pocket where CO binds to the heme iron. One can see that the CO begins to move away from the Fe atom once the bond is broken (purple structure).

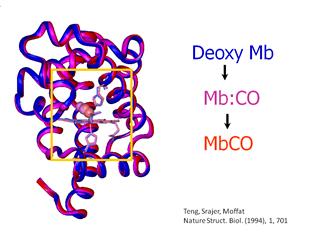
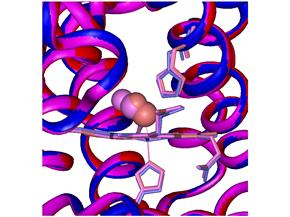
Figure 3. Superimposed cryogenic forms of myoglobin combined with the diatomic molecule CO.

1. Spectroscopy of the heme group in myoglobin

The heme group in myoglobin is a useful probe of the state of the protein. Figure 4 shows that the carbonmonoxy (CO) form and has a different spectrum than the deoxy form. The figure shows that there are intense B bands and weak Q bands for both forms. The reason for these two types of electronic transitions can be found in the simple particle-on-a-circle model. In that model, we have shown that the energy levels of the porphyrin can be modeled using an 18-electron p-system shown in Figure 5. Starting with the energy levels of the particle-on-a-circle given by the Schrödinger equation,

(.1.2)

We have the normalized solutions

(.1.3)

where

Figure 5 shows us the meaning of these quantum numbers. They refer to whether the electron is travel clockwise m > 0 or counter-clockwise m < 0 around the circle. Moreover, we can understand the selection rule based on our study of the interaction of electric fields with matter. The electric fields polarized along x- and y- are

(4)

Thus, a transition dipole moment operator that connects two states under the influence of the electric field also has the form

(5)

where e is the charge on the electron. Only if the transition dipole moment is non-zero will the electric field be able to interact with the molecule. For example, the x-polarized transition dipole moment is

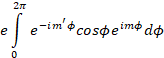(6)

Where m and m’ are different quantum numbers. We see from Eqn. .1.5 that we can write this as

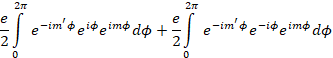
(7)

The condition for the integrals to be non-zero are

or

This condition or selection rule is shown in Figure 5. It is also shown that the number m corresponds to the number of nodes in the wave function when a more advanced molecular orbital picture is applied to understand the spectroscopy. It turns out that any level of quantum theory predicts that the ground state of heme (or any porphyrin) consists of two states that are so close in energy that they act as thought they were degenerate. These are shown a_1u and a_2u in Figure .5. The excited state is a rigorously degenerate e_g set of levels. Putting these together gives two possibilities for the p-p* transition. There are two transition moments (M₁ and M₂ in Figure 5) that can add constructively, M₁ + M₂, to give the intense B band or destructively, M₁ - M₂, to give the weak Q band. Both the B band and the Q band provide a means to monitor changes in the ligation state of the heme iron. Figure .5 shows that the difference in the CO-bound form MbCO and the deoxy form Mb is significant. We can use these spectral differences to monitor the rebinding of CO heme proteins. This is a spectral probe of ligand dynamics that also teaches us about protein dynamic motions.

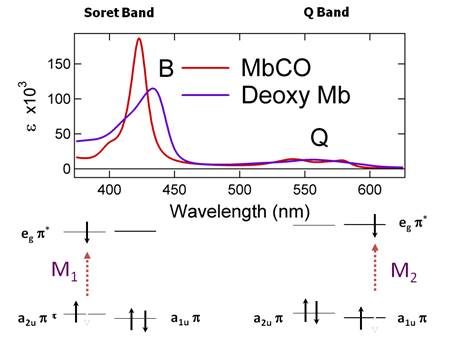
Figure 3. Soret (B) and Q absorption bands for heme. The energy level

scheme for heme is shown below. There are two transitions that can

add constructively or destructively.

When comparing the free electron model we note that there is a “forbidden transition” with Dm = 9 that is predicted by the particle-on-a-circle or free electron model. The Q-band is this forbidden transition. Since the Q-band is observed, there must a mechanism that makes the forbidden transition allowed. We can this mechanism vibronic coupling. Distortions along normal modes of vibration can lower the symmetry of the molecule and permit a weak, but still observable band in this region. It is worth noting that when the metal has no spin contribution, the change in the orbital angular momentum of the Q-band is 9 times larger than that for the Soret band. This means that the simple free electron theory correctly predicts the magnetic behavior of this band.

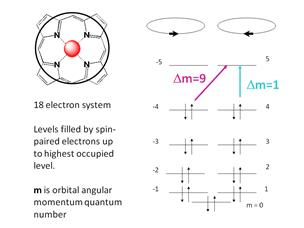
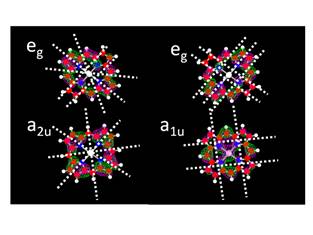
Figure .5. Comparison of the free electron model with a full quantum chemical calculation of the molecular orbitals of the HOMO (p) and LUMO (p*) orbitals of heme.

.1.3 Kinetics of myoglobin

The kinetics of CO recombination have been studied using flash photolysis. Once the Fe-CO bond is broken, the CO can migrate out of the pocket shown in Figure 3. At room temperature the CO can escape into the solvent. Thus, there are two possible pathways for the -CO to recombine with the iron. There is a geminate pathway (direct recombination from within the protein), and a bimolecular pathway, which involves migration back into the pocket. The kinetic scheme,

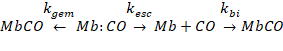
(8)

An approximate solution of the rate equations leads to the time course for the disappearance of the deoxy Mb form following photolysis.

(9)

where the prime indicates that this is a pseudo-first-order rate constant, . If the experiment is done under conditions where [CO] is in excess in solution, we can ignore any changes in [CO] concentration. Under these conditions we can follow both the geminate phase on the nanosecond to microsecond time scale and the bimolecular phase on the millisecond to second time scale as shown in Figure .7.

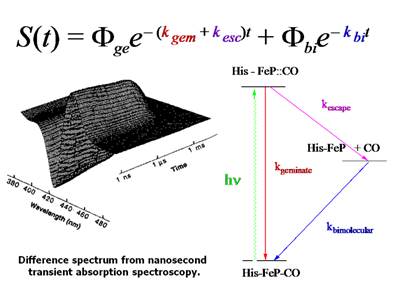
Figure 5. Kinetic scheme for CO photolysis and recombination in myoglobin.

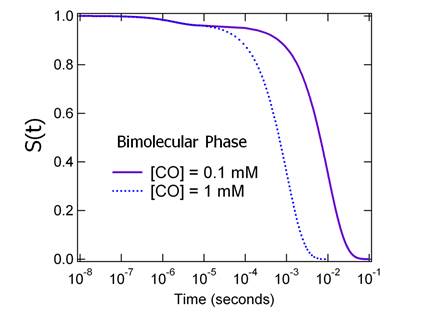
Figure 6. MbCO recombination kinetics.

The factors that control the geminate process include the iron spin state and geometry in the heme iron. For example, for MbCO the iron is six-coordinate and low spin (S = 0). When the CO is photolyzed the iron becomes five-coordinate and high spin (S = 2). The change in spin state correlates with a change geometry. The iron is large in radius when the electrons are unpaired and the result is that iron no longer fits in the center of the heme porphyrin ring the S = 2 state. Consequently, the iron moves out of the plane as shown in Figure .8.

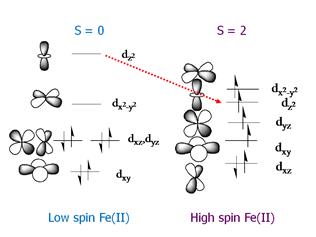
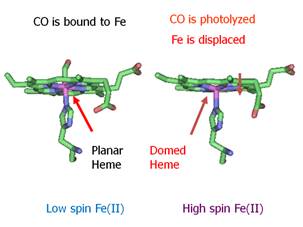Figure 7. Correlation of spin state with structure in heme complexes.

The recombination of CO with the iron is thermodynamically favored, but is kinetically rather slow because of the requirement for a change of spin state. Figure .9 shows the calculated MbCO (S = 0) and deoxy Mb + CO (S = 2) states. There is a barrier at the intersection.

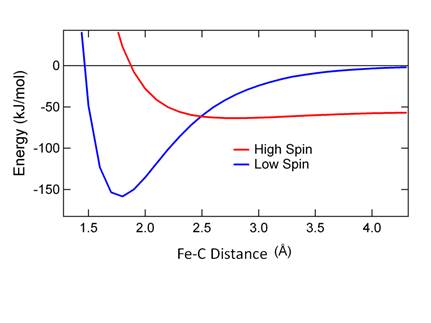
Figure 8. Potential energy surfaces for MbCO recombination.

.1.4 The H93G cavity mutant

There are literally hundreds of biophysical studies of myoglobin. The kinetics of myoglobin has been studied as an example of protein dynamics. One aspect is the recombination kinetics of photolyzed CO at low temperature or high viscosity. Under these conditions the recombination becomes non-single-exponential. We have seen that first order kinetics are single exponential. However, more complex kinetic decays are often observed experimentally. What does it mean if a kinetic time course is not single exponential? One possible interpretation is that there are multiple intermediates in a sequential pathway. We have already discussed the case one intermediate (see section .1.3). We can further consider two intermediates as shown below.

MbCO à Mb:CO(1) àMb:CO(2) à Mb + CO

As a general rule the number of exponentials needed to describe such as a system is equal to the number of intermediates plus one. Here it would be three exponentials. Obviously, the time scales for formation of each intermediate would need to be sufficiently distinct to permit the observation of unique times.

A second possibility that might give rise to non-exponential kinetics is the existence of different protein structures. This idea has been used to suggest that myoglobin exists in many different conformational states (and even substates) so that non-exponential kinetics represent many different recombinations with different rate constants. It was thought that the iron out-of-plane displacement played a key role in these states and the associated rate constants.

One way to test the role of the iron is to use a proximal cavity mutant. Histidine 93 is the amino acid that binds to the heme iron. The mutation to glycine abolishes this connection between the heme iron and the protein. Instead, the protein is grown in E. coli with an exogenous iron ligand, such as imidazole. The net effect is a protein shown in Figure .10, which differs from the wild type only by one carbon atom. The b-carbon that normally connects the imidazole ring of the histidine to the protein is missing in H93G. This carbon is shown by the red circle in the Figure .10. It is evident that the carbon atom is missing in the mutant. The imidazole in the mutant can be replaced by other imidazoles and even pyridines or other coordinating ligands that fit into the cavity. The kinetics of three different imidazoles are shown in Figure .10 as well.

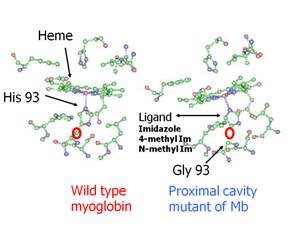
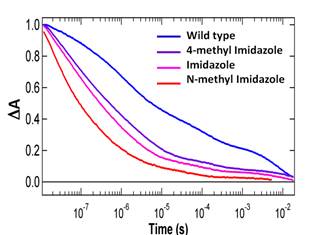
Figure 9. Structure and kinetics of H93G-CO.

One conclusion that can be drawn from the data in Figure .10 is that the kinetics can change dramatically with no intervention by the protein. The proximal ligand in H93G is not covalently bound to the protein. Thus, the large change in kinetics in Figure .10B is not the result of protein control, but rather a chemical effect that arises from the bonding. The kinetics shown in Figure .10B were obtained at 250K. This means that the geminate phase is large. At 250K in 50% glycerol/buffer the protein is frozen and ligand escape shown in Figure 5 is very limited. The fact that the kinetics are highly non-exponential in all of these cases would, by itself, seem to indicate that the Fe-control hypothesis is not the correct one to explain the lack of exponential kinetics. Rather the kinetics are probably determined by multiple geometries (conformations), which could arise from either a parallel or sequential model, as discussed above.

It might be objected that the proximal has some kind of effect on the kinetics on the distal side. Such a feedback could occur if the geometry on one of the heme were communicated through the protein structure to the other side. One can perform a kinetic analysis of the geminate and escape rates from data such as those shown in Figure .10B to determine whether the escape rates are affected or mainly the geminate rates (Table 1).

Table 1. Experimental data for the observed recombination of CO to H93G mutant proteins.

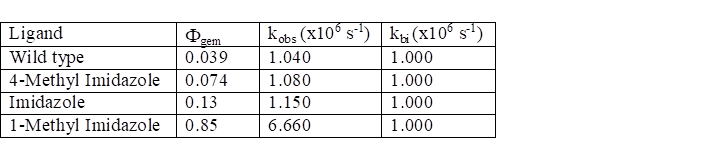
The data in Table 1 were obtained at room temperature. Note that the measured parameters must be analyzed using Eqn. 9 in order to obtain the intrinsic rate constants, k_gem and k_esc. The results supported the hypothesis that the proximal ligand mainly affects the geminate rate. The escape rates showed a modest effect as a function of the ligand. The analysis of these rate constants is given as an exercise below.

.1.5 Vibrational spectroscopic studies of MbCO

The internal environment of the protein can be probed using the infrared stretching frequency of both Fe-bound and unbound carbonmonoxide (CO). The Fe-CO adduct has significantly different properties from free CO. In the gas phase, the CO stretching frequency is 2143 cm^-1. However, just as vibrational mode frequencies of H₂O are shifted in the liquid because of hydrogen bonding, we observe that CO will have a shifted frequency when it is trapped in a protein (e.g. 2110 cm^-1 – 2135 cm^-1). The shift is relatively small compared to that of water, which is a result of the weaker hydrogen bonding.

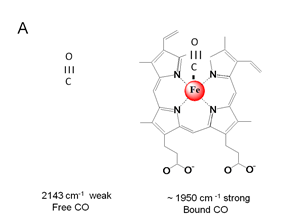
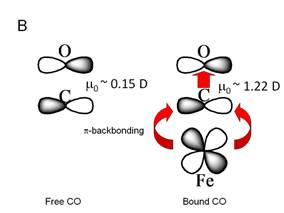
Figure 10. A. Depiction of free and heme-Fe-bound CO. B. illustration of the dipole moment of free CO and the effect of p-backbonding interaction on the dipole moment of bound CO. The p -backbonding interaction strengthens the Fe-C bond and weakens the C-O bond.

The chemical bond formed when CO makes and adduct with the heme iron has a profound effect on both the frequency and the infrared intensity of CO. This is illustrated in Figure 20. The frequency lowering of the n(C-O) stretching vibration shown in Figure 10A is due to the fact that the Fe-dxz,yz orbitals add electron density to the p* orbital of the CO. Thus, the strengthening of the Fe-C bond occurs at the expense of the C-O bond. This shift is observed in all heme proteins, but the magnitude of the shift depends on the nature of the trans bonding to the heme Fe atom. The values of n(C-O) range from 1910 cm^-1 to 1980 cm^-1 depending on the proximal ligand and on the nature of distal interactions. The distal interactions can be thought of as hydrogen bonding between amino acids the bound CO molecule. These interactions too will have an effect that can be as large as the proximal effect. Such effects can be studied selectively by site-directed mutagenesis of the distal pocket as shown in Figure 11.

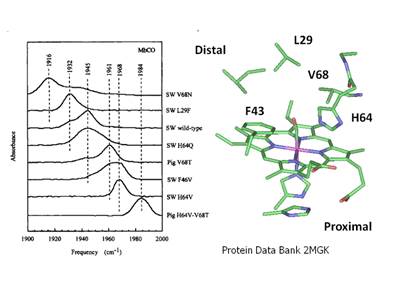
Figure 11. The effect of site-specific mutations on the frequency of Fe-CO in Sperm Whale myoglobin. Note that the frequency of the n(C-O) stretching band ranges from 1916 cm^-1 to 1984 cm^-1. Depending on its hydrogen bonding environment.

The effect of bonding can be seen as an effect on the force constant. Since the reduced mass is constant for the entire series in Figure .12 we can study the effect of the hydrogen bonding as the effect of an applied electric field on the vibrational frequency, a so-called vibrational Stark effect. This type of effect provides information on the conformations of heme proteins and particularly, it is the effect near the active site that is most relevant.

The infrared absorption intensity of the CO is increased by nearly a factor of 20 when it is bound to the heme iron. We can understand this as an increase in the ground state dipole moment, m. If m is larger then the infrared transition moment, which is proportional to will also be larger. The increase in dipole moment comes about because of the additional effect of the electron density from the Fe atom. We can estimate m in the bound state based on the additional charge injected by the heme iron. This effect is observed experimentally in low temperature infrared difference spectra shown in Figure 11. In the experiment shown in Figure .13 the sample is cooled to below 20 K. Then an infrared spectrum is taken. Subequently the sample is irradiated to photolyze CO. A second infrared spectrum is taken, and the first spectrum is subtracted from the second to create a difference spectrum. In the difference spectrum, any bound CO will appear as a negative band and any photolyzed CO will appear as a positive band. We see in the Figure that the intensity of the negative band (corresponding to Fe-C-O) is nearly 20 times larger than that of the positive band (corresponding to photolyzed CO trapped in the protein).

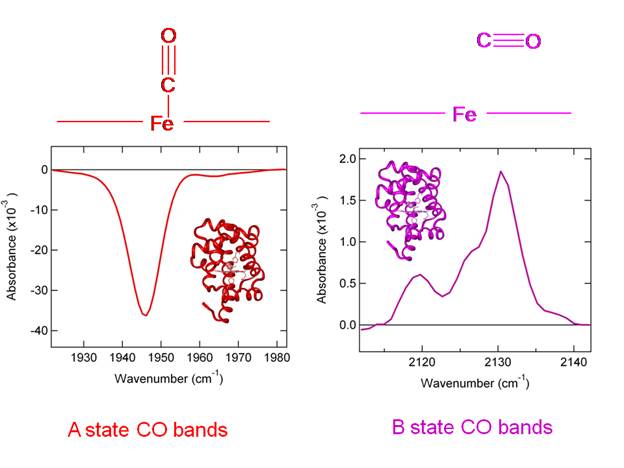
Figure 12. Experimental evidence for a difference in intensity between bound and free CO. The bound CO species can have multiple frequencies due to different conformations of the protein, known as A states. Likewise, the CO bands of free CO trapped in the protein are known as B states.