Sedimentation and centrifugation

Sedimentation

A particle falls in a solution of density ρ and has a specific volume .  The specific volume of the particle is the inverse of its density and has units of ml/g (or L/kg or m3/1000 kg).  If the product v2r < 1, then the particle will sink.

 

Sedimentation is used to separate, purify and analyze proteins, oligonucleotides, cellular structures and viruses.  We consider first the sedimentation in a gravitational field.

 

                                                                                                                                                (1)

If we assume that there is a frictional force f and sedimentation velocity u, we have:

 

                                                                                                                                                (2)

When the particle has reached the terminal velocity (it is falling as fast as it can) then the acceleration du/dt = 0.  Therefore,

                                                                                                                                                (3)

and

                                                                                                                                                (4)

In a centrifuge the acceleration is ω2x, where w is the angular frequency and x is the distance from center of rotation x. 

 

                                                                                                                                                (5)

The quantity u / ω 2x is the velocity per unit acceleration.  It is called the sedimentation coefficient s.  The definition of s is:

 

                                                                                                                                                (6)

As we have seen before the friction coefficient is f = kT/D .  Using the  fact that M = mNA we can solve for the molar mass in terms of s, D and v2.

 

                                                                                                                                                (7)

s20,w is the corrected value of the sedimentation coefficient to give the expected value in water at 20 oC.   Since the viscosity and density of water are temperature dependent it is important to have a standard for comparison.  This is the role played by the standard sedimentation coefficient.

 

                                                                                                                                                (8)

 

Application of the Boltzmann relationship to a gravitational potential

We have seen that the relative probability of particles or molecules being in two levels separated by an energy ΔE is:

                                                                                                                                                (9)

For example if we consider a molecule in the atmosphere its molar potential energy is:

 

ΔE = mgh

                                                                                                                                                (10)

If we subsitute this expression into the Boltzmann relation we find:

 

                                                                                                                                                (11)

where M is the molar mass.  Note that this is the barometric pressure formula!

In a viscous medium the energy as a function of height is given by:

ΔE = m(1 – v2ρ)gx

                                                                                                                                                (12)

If we subsitute this expression into the Boltzmann relation and express it in molar units we find the relative concentration of a molecule as a function of the height x in a container.

 

                                                                                                                                                (13)

 

Equilibrium centrifugation

In a centrifuge the gravitational constant g is replaced by the centrifugal acceleration ω2x.

 

ΔE = m(1 – v2ρ)ω 2x2

                                                                                                                                                (14)

The concentration as a function of distance form the center of rotation is given by:

 

                                                                                                                                                (15)

In equilibrium sedimentation a gradient is created by the acceleration of the centrifuge.  An example is CsCl density gradient centrifugation.  In such an experiment the macromolecules will be found at the location in the gradient where they are bouyant. The molecules that were initially uniformly distributed throughout the solution will concentrate at the point where their partial specific volume is equal to 1/ρ where ρ is the density of the salt solution.

 

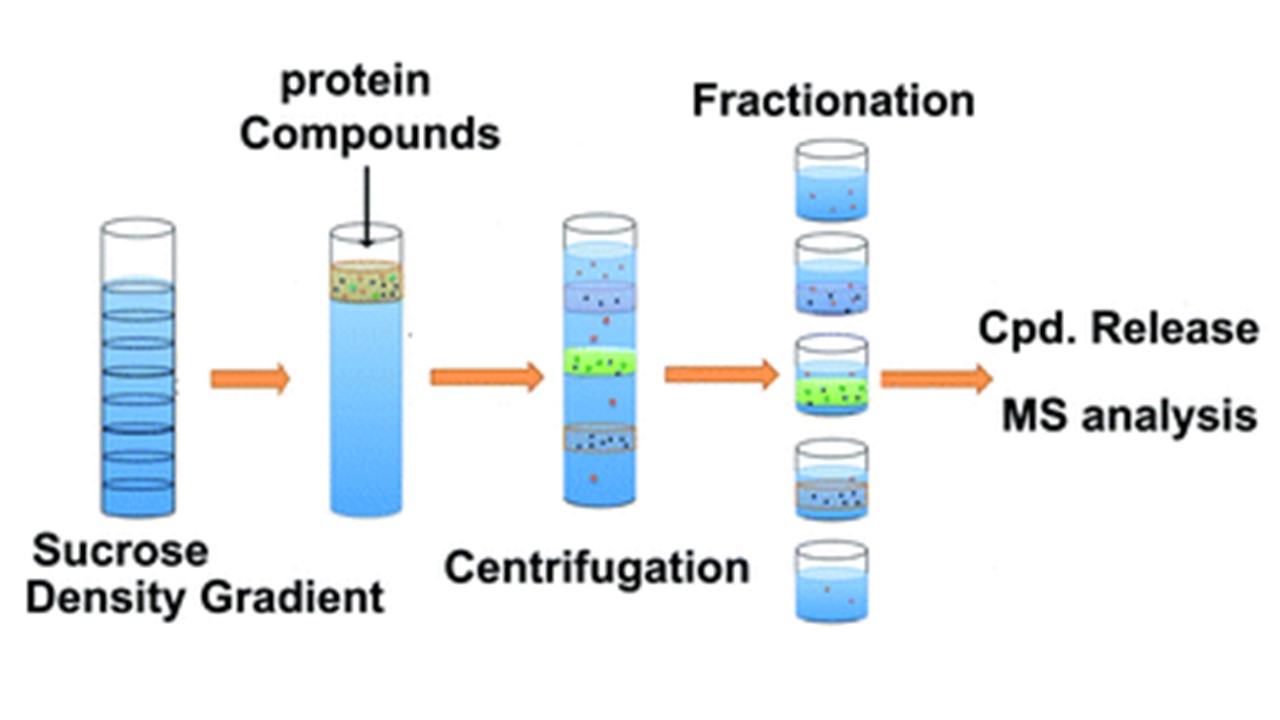
The figure shows how a sucrose density gradient is used to separate proteins or other samples with different densities. They settle out att different heights in the gradient and then can be separated one the centrifuge is stopped. This must be done quickly and carefully, of course.