We have seen that electromagnetic radiation can promote transitions between electronic energy levels in hydrogen and other atoms. The same is true in molecules where there are transitions possible between molecular orbitals. Molecular motions can also give rise to the absorption of radiation. Infrared radiation is absorbed because of molecular vibrations. Vibration can cause a change in the dipole moment of the molecule. The oscillating dipole moment can interact with electromagnetic radiation at the appopriate frequency.
Rotational motions and spectroscopy
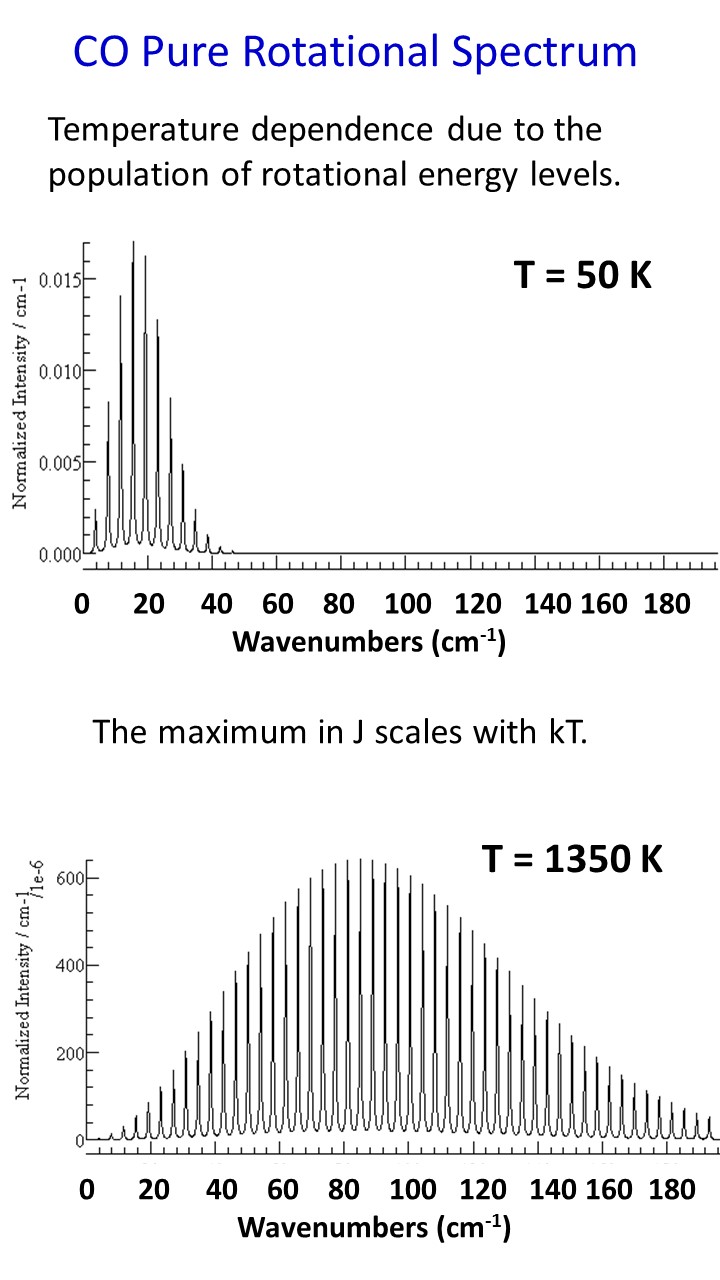
The classical picture of rotational spectroscopy involves the interaction of light with the rotating dipole moment of the molecule. We usually assume that the internal coordinates of the molecule are fixed. This is known as the rigid rotator approximateion. Then we imagine observing the molecule rotate from a fixed direction of observation. We would see the dipole moment oscillating. In the classical picture microwave radiation is absorbed because the molecular dipole rotates with a frequency that is conincident with microwave radiation. The quantum mechanical solution for the rotational problem in three dimensions gives wave functions that are called spherical harmonics. These are standing waves on a sphere. The wave functions have the appearance of the s, p, d, f etc. functions for the electron in the hydrogen atom. This is because the two problems are mathematically identical. The physics of rotation is different, however, and the square of the spherical harmonics describe the probability for the molecular dipole as it rotates in a quantum mechanical sense. The solutions predict that the energy levels will increase EJ = B J(J+1) where B is the rotational constant and J is an integer. Since the selection rule is Delta J = + or - 1, the pure rotational spectrum is a series of lines with a spacing of 2B as shown in the figure below. Because the spacing of the rotational energy levels is significantly less than kT at 300 K, there is a dramatic change in the population of levels as the temperature changes through room temperature. This is also shown in figure below for carbon monoxide (CO). The line spacing for CO is approximately 3.86 cm-1, which gives a rotational cosntant of 1.93 cm-1.
Vibrational motions and spectroscopy
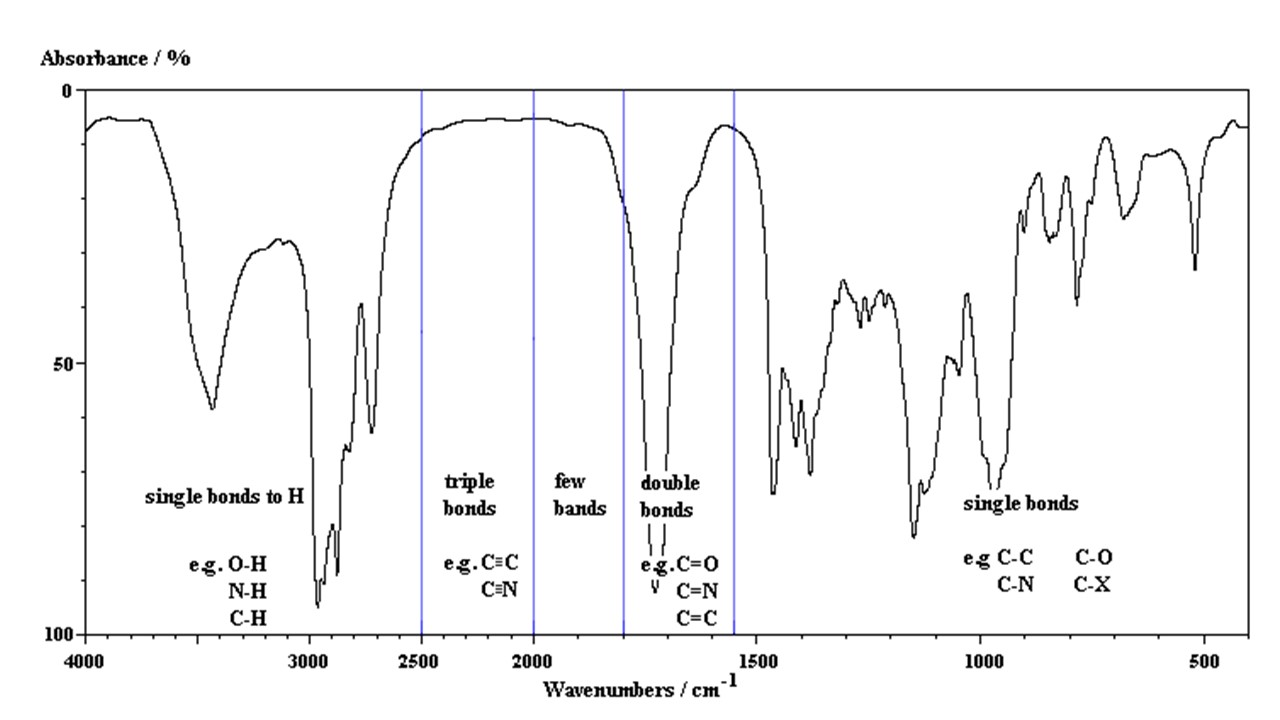
For molecules that have a change in dipole moment during their vibrational motion there can be absorption of infrared light. In the classical picture, the frequency of molecular vibrations is coincident with the frequency of infrared light, which permit the absorption of IR light. Harmonic motion in classical physics assumes a Hooke's law force F = -kx. The potential energy is V = 1/2 kx2. The quantum mechanical harmonic oscillator uses the same harmonic potential as the classical harmonic oscillator. However, the quantum solutions are Gaussians time polynomrials and they represent the localization of the nuclei. The classical solutions are cosine functions that represent the periodic motion. The concrete difference is that the classical motion has a deceleration near the classical turning points at the end of the range of motion. The quantum mechanical solution in the lowest state (v = 0) is localized at the equilibrium position. This is an important result since the localization of the nuclei at the equilirium position makes physical sense. The energy solutions are Ev = (v + 1/2)h nu. The difference between any two successive energy states is just Delta E = h nu and there is only one vibrational transition observed. In the harmonic approximation the infrared spectrum is a single band. This property of the spectra makes fourier transform infrared (FTIR) spectra very useful for numerous applications. The organic chemist will use FTIR spectra as a fingerprint method for rapid testing of progress in synthesis. The various regions of the FTIR spectra are labeled in the figure below. Protein FTIR analysis is discussed in the section on FTIR spectroscopy to the right.
Rovibrational spectroscopy
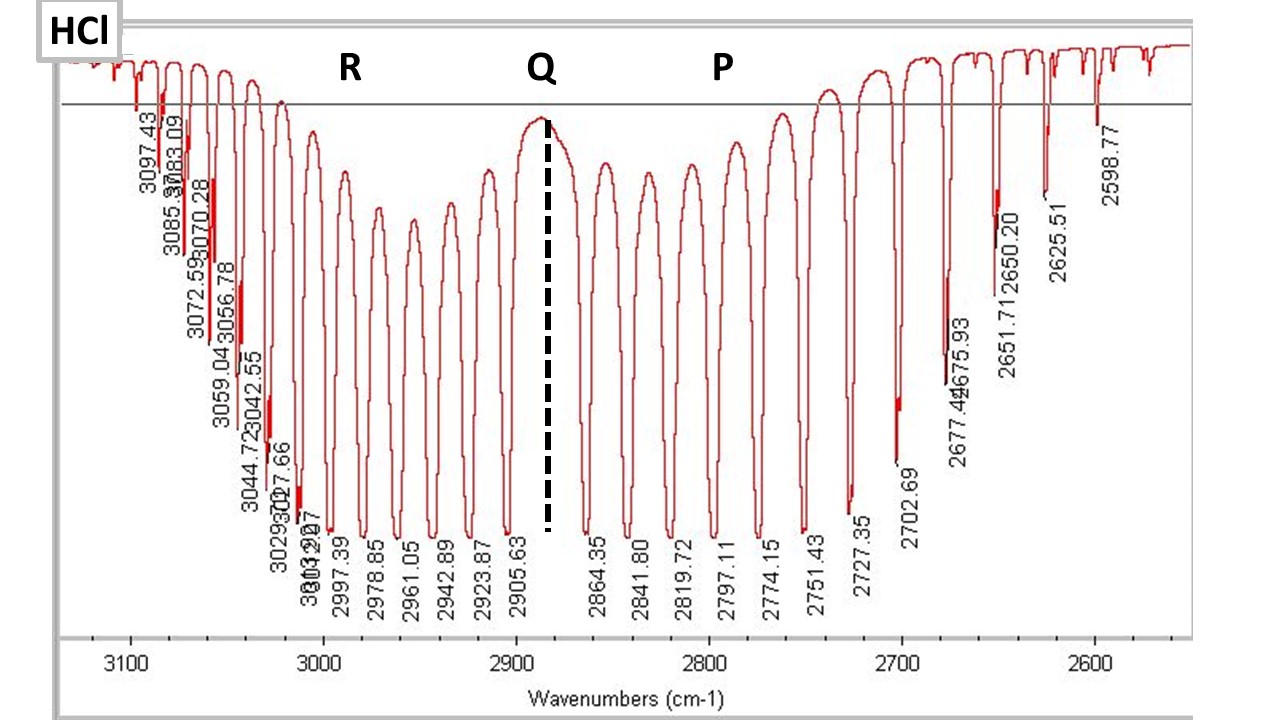
Rovibrational spectra can be observed in the gas phase. When molecules can have both vibrational and rotational transitions the spectra must follow the selection rules of both. This gives rise to a series of rotational lines to lower energy than the main band (the P branch) and to high energy (the R branch). These series of lines have a change of rotational quantum number of J - 1 and J + 1, respectively. The Q branch is the central line, which is not observed since Delta J = 0 is not an allowed transition. Rovibational spectroscopy is the most useful gas phase method for identifying molecular properties in a simplified way. The study of HCl shown in the figure below is a classic laboratory experiment. From a fit of the spacing of the liens in the P and R branches one can calculate the anharmonicity and centripedal distrortion of HCl. One can perform a linea, quadratic and even cubic fit to extract these parameters from experimental data. Because of the wealth of information available gas phase spectroscopy is a very powerful method for understanding details of chemical reactions. Molecular beams can be used to direct a flow of molecules to the zone of observation and to monitor various quantum states during the course of a reaction.
|